
数学原理
矩阵维度与运算的理解
在多维(三维四维)矩阵向量运算-超强可视化这篇文章中,提到了张量运算的可视化方法,现做一些总结。
在Keras框架中,生成一个矩阵/张量,可以采用以下方式。
二维,输出一个两行三列的矩阵。
1 | import keras.backend as K |
输出为:
1 | [[1. 2. 3.] |
三维,同样的代码,只是shape有所改变。
1 | a = K.constant(np.arange(1, 13), shape=[2,2,3]) |
输出为:
1 | [ [ [ 1. 2. 3.] |
四维,同样的代码,只是shape有所改变。
1 | a = K.constant(np.arange(1, 37), shape=[3,2,2,3]) |
输出为:
1 | [ [ [ [ 1. 2. 3.] |
仔细观察输出,可以发现如下现象:
shape的长度决定了输出的向量前面几个[开头,后面有几个]结尾。
二维的输出结果作为一部分出现在了三维的输出结果中,三维的输出结果作为一部分出现在了四维的输出结果中。由此,可以看出上面例子中的三维结果是由2个二维结果拼接在一起的,这里2个是由shape=[2,2,3]中的第一个2决定的,而[2,3]决定的是二维矩阵是几行几列的。同样的道理,上面例子中的四维结果是由3个三维结果拼接在一起的,这里的3个是由shape=[3,2,2,3]中的第一个3决定的。可以看出,shape的第一个数字只是当前维度n的上一个纬度n-1维度的排列个数。
这里有一种递归的思想在里面,n维的矩阵,无论怎么排,最终都会递归到2维,因为2维是构成矩阵的最小维度。
既然如此,高维矩阵的运算,归根结底是2维矩阵的运算。两个高维矩阵中对应到2维矩阵的部分现做矩阵运算,结果再度拼为高维矩阵即可。而2维矩阵总是由shape中的最后两个维度决定的,只要最后两维度满足匹配原则,就可以正常运算。
shape=[2,2,3]与shape=[2,3,4]的两个矩阵进行矩阵乘法运算。
1 | a = |
执行如下语句进行矩阵乘法。
1 | c = K.batch_dot(b, a) |
结果为如下。
1 | [[[ 38. 44. 50. 56.] |
可以看出
1 | [[ 38. 44. 50. 56.] |
其中,38就是第一个矩阵的第一行与第二个矩阵的第一列对应位置相乘并相加的结果。
从Keras提供的矩阵想成的方法也可以看出,这是二维矩阵的批量运算batch_dot。二维矩阵使用K.dot(a, b)即可;对于高维矩阵,引入batch matrix multiplication的方法,使用K.batch_dot(a, b)进行运算。
Data is considered as (B1,…,Bn,C,H,W) format. Spatial dimension of tensor is in the last two indices.
The multiplication has been performed considering (2) as the batch size or non-spatial dimension, and spatial dimension of tensor a is (2,3) and b is (3,4).
这里的解释来自A brief talk through Matrix Multiplication in Keras with Tensorflow as Backend。
Numpy中的ndarray于tensor的联系
在事实上,numpy中也有ndarray类型的数据,意思就是n-dimensional array。它的表现形式和张量类似。
具体查看这篇博客A Visual Intro to NumPy and Data Representation这篇文章中,讲述到了Numpy中ndarray的表现形式。
ndarray就是N-dimensional array的意思。要让numpy生成高纬度的矩阵,只需要在初始化一个矩阵的时候多几个维度即可,如np.ones((4,3,2))。
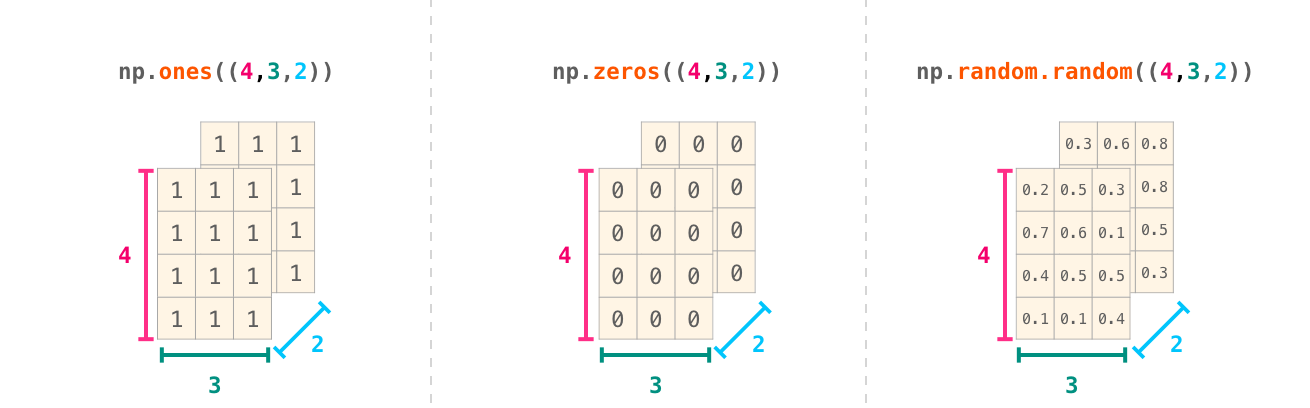
正常的理解思路是我们有4行3列的矩阵,两个堆叠在一起。
但是numpy在输出ndarray的时候却不是按照这个思路进行的。传入的维度(d1,d2,d3…,dn),numpy最先考虑的是最后一个轴dn的循环打印,然后依次从后往前,最后才考虑第一个轴d1的打印。
因此就会有如下的输出:
1 | array([[[1., 1.], |
可以看出,上面的输出是我们对上一张图从上往下看所见到的每一个层。
- 本文标题:机器学习中的矩阵基础
- 本文作者:徐徐
- 创建时间:2020-10-28 09:41:36
- 本文链接:https://machacroissant.github.io/2020/10/28/matrix-calculus-tips/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!