
深度学习三个步骤
Neural Network
前馈feedforward,输入进入网络后流动是单向的。两层之间的连接并没有反馈feedback。
全链接fully connect,每一层之间两两都有链接。
Input Layer输入层 1层— Hidden Layer 隐藏层 N层 — Output Layer输出层 1层。
Deep = many hidden layers
Goodness of function
单个训练样本
采用损失函数Loss function来反映模型的好差,利用交叉熵函数对$y$和$\hat{y}$的损失进行计算。
注意损失函数是定义在单个训练样本上的(在表达式上使用下标,且使用小写的$l$)也就是一个样本的误差。
所有训练样本
总体损失函数Total loss function是所有样本的误差的总和。也是反向传播需要最小化的值。
注意这里的$x^i$不是一维的数据,是用来表示一个对象的多维度向量,$x^i$和$x_i$表示的对象不相同,注意区分上下标。
注意是吧所有训练数据的损失都加起来得到的总体损失L。为了最小化这个损失L,也就是要在function set里面找一个最优函数,也是酒找神经网络中的参数$\omega$。
Pick best function
使用梯度下降。
Back Propagation: an efficient way to compute $\partial{L}/\partial{\omega}$ in neuron network.
反向传播
反向传播是在使用梯度下降计算参数变化量的时候,让求梯度更方便的一种方法。
反向传播背后的数学原理就是链式法则。
因为单个样本的loss function是关于系统输出$y$的函数,输入$x$通过系统一层层传递才到输出$y$,所以链式法则拆分的时候也是拆阶段性结果做微分。
单个训练样本分析
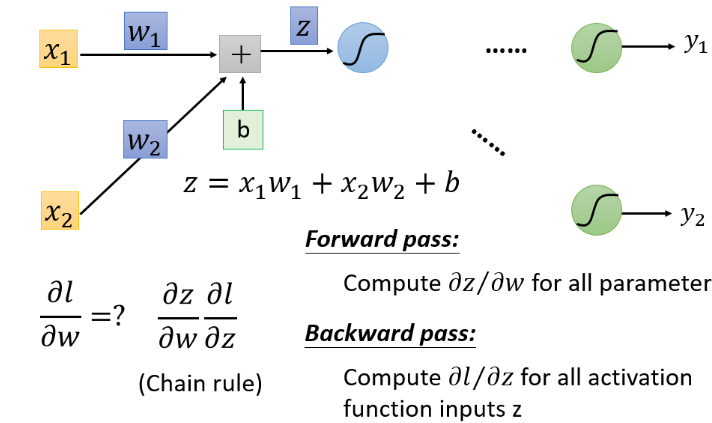
输入先进入一个由权重weight和偏移b组成的线性系统获得线性函数输出z。
线性输出z进入一个激励函数non-linear activation function获得一个非线性输出,该输出作为下一层神经网络的输入。最常用的非线性激励函数就是Sigmoid Function。
为什么需要激励函数?用于加入非线性因素。因为有些数据线性可分,但是某些数据线性不可分。
计算$\frac{\partial z}{\partial \omega} $就是Forward Pass的过程,结果就是the value of the input connected by the weight,该层神经网络的输入。此处需要注意z已经在forward pass中被确定了。
计算$\frac{\partial l}{\partial z}$就是Backward Pass的过程。运用链式法则的时候需要注意,最终结果$\partial l$是和$\partial y$结合在一起的,而$\partial y$是作为non-linear activation function的输出存在的,而该非线性激励函数的输入又是$z$,即该层神经网络的输入经过线性变换之后得到值。
Mini-Batch
相关参数batch_size和nb_epoch。
实际操作并不总是对所有样本最小化总的损失函数,而是将数据随机分成几个mini-batch,每个batch的batch_size指定之后,可以根据有多少样本算出有多少个batch。
初始化神经网络参数后,随机选择第一个bacth的样本,对它计算total loss,然后更新神经网络参数;第二个batch..……直到选了batch_size个batch的样本,也就是对神经网络的参数更新了(总样本数/batch_size)次,才能称做遍历了一次nb_epoch。
batch_size代表一个batch有多大(就是把100个example,放到一个batch里);nb_epoch等于20表示对每个batch重复20次。
Tips for Deep Learning
在完成深度学习的三个步骤,得到神经网络之后,需要首先考虑是否能在训练集上获得好的表现。
如果在训练集上不能获得好的表现,需要从Adapative Learning Rate和New Activation Function两方面考虑。
如果在训练集上表现良好,但是在测试集上表现差,说明是overfitting,从Early Stopping和Regularization以及Dropout三方面考虑。
训练集表现不好
Vanishing Gradient Problem
梯度消失是在使用Sigmoid Function作为激励函数时存在的问题。
依据Sigmoid Function的图像来看,它将输入输出都限定在0~1范围内,随着输入增大靠近一条渐近线。
当网络比较深,Sigmoid Function的输入值比较大的情况下,每一次对输入值做的变动delta,都会在输出上表现为很小的变动delta,从而靠后的hidden layer对loss的影响非常小。
如何解决梯度消失的问题?
有两个方式,一是动态调整学习率,二是直接更改激励函数。
更改激励函数
ReLU激励函数
input>0, output=input; input<=0, output=0.
对于input>0的范围,在input比较大且变化比较的地方,梯度下降比较快,可以处理梯度下降问题。
对于input<=0的范围,那些output=0的部分直接可以从整个网络中拿走。最后整个网络就变成了thinner linear network。
改进1: Leaky ReLu
改进2: Parametric ReLU
以上改进都是在input<=0的情况下通过乘以一个比较小的参数让output有一点值。
改进3: Maxout/Learnable Activation Function
应该是先对每一层的neuron进行group,每一个group后的结果z都是max{group member result z},对于所有input的可能取值,就相当于线性规划出了一个linear convex function。group的数量越多,那么convex的角就越多,激励函数也就越复杂,更直观地变成了非线性。
该如何训练该网络?一方面,max过后,该网络就相当于剪枝了,另外一个线性变化后的z就不需要考虑了,最终还是得到thinner linear function。另一方面,对于较全的训练集input,应当max函数中的每一个weight和bias过后的z都会成为max过后有效网络的一部分。
动态调整学习率
PMSProp/Root Mean Square Prop
Adagrad中也提出了动态调整学习率,Use first drivative to estimate second derivative。用固定的learning rate除以这个参数过去所有GD值的平方和开根号。
Root Mean Square of the gradients with previous gradients being decayed.
$\alpha$值调的小一点,说明倾向于相信新的gradient指示的error surface的平滑程度/陡峭程度。
local minima的解决
当神经网络很大,参数越多,出现local minima的几率越低。
联系物理中的惯性,每次移动的方向,不仅考虑某一点的gradient,还考虑前一个时间点移动的方向movement of last step,将这两者求矢量和。
对于某一个点$\theta^i$,此处有movement为$v^i$,对该点计算gradient得到$\nabla{L(\theta^i)}$,那么下一次移动的方向movement为$v^{i+1} = \lambda v^i - \eta \nabla{L(\theta^i)} $。如果递推下去,可以有
$v^i$ is actually the weighted sum of all the previous gradient.越之前的gradient,对此刻的movement影响越小,越多考虑目前的gradient的影响。
Adam = RMSProp + Momentum
测试集表现不好
注意这个是在训练集表现良好的基础之上进行的。
此处的测试集是cross validation中从原训练集中抽取出来的validation set。
Early stopping
虽然训练集在loss降低,但测试集上有可能loss降低后又升高了。需要让epoch停留在测试集的最低点。
Regulariazation
通过给原损失函数添加一个Regularization Term,构成一个新的需要最小化的损失函数。目的是weight decay,closer to zero。
L2 Regularization
Regularization Term = $\lambda \frac{1}{2} \left|\theta\right|_2$
$\left|\theta\right|_2 = (\omega_1)^2 + (\omega_2)^2 + \cdots$
对新的损失函数求微分且合并同类项后可以发现,对已有weight$\omega^t$总是乘上总小于1的$(1-\eta\lambda)$,相比于之前的乘以1,目的是让weight更接近0。是基于已有weight的。
L1 Regularization
Regularization Term = $\lambda \frac{1}{2} \left|\theta\right|_1$
$\left|\theta\right|_1 = |\omega_1| + |\omega_2| + \cdots$
对新的损失函数求微分后发现不可合并同类项,只是减了一个$\eta\lambda sgn(\omega^t)$,每次减的都是固定值。
Dropout
训练时,每次在更新参数之前,让每个neuron都有p%的几率dropout,然后使用new thinner network去训练。for each mini-batch, resample the dropout neurons。在加上dropout之后,training set上的测试结果会变差。
测试时,不做dropout,训练时的dropout rate是p%,则测试时所有的weight都乘以(1-p)%。
为什么dropout会有用?
Dropout is a kind of ensemble. 就相当于把训练集分成了好多个子集,每个子集都生成一个network。当把testing data都分别放入这些网络的时候,每个网络都会给出一个结果,最终给这些结果去一个平均值。
why deep
深度学习其实就是模组化。
每一层neural可以被看做是一个basic classifier,第一层的neural就是最基分类器;第二层的neural是比较复杂的classifier,把第一层basic classifier 的output当做第二层的input(把第一层的classifier当做module),第三层把第二层当做module,以此类推。
例子:语音辨识/逻辑电路
similar input — different output / different output — similar output
- 本文标题:深度学习总介绍
- 本文作者:徐徐
- 创建时间:2020-11-03 08:42:45
- 本文链接:https://machacroissant.github.io/2020/11/03/back-propagation/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!