
Linear SVM model
Step1: Function Model
Step2: Loss Function
Loss function的第一项是一个凸函数,第二项也是个凸函数,因此loss function整体也是凸函数。有不可微分的地方,但是可以用梯度下降做优化器。第一项的定义涉及了loss function,也就是Hinge Loss的方法。
第一项中的
Step3: Gradient Descent
第一种理解
做微分,先不考虑第二项。
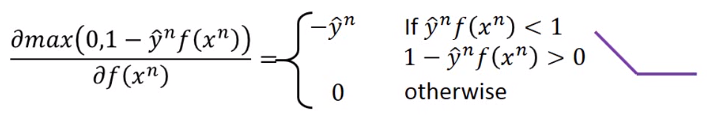
第二种理解
用一个极小项

Kernel Method
Dual Representation
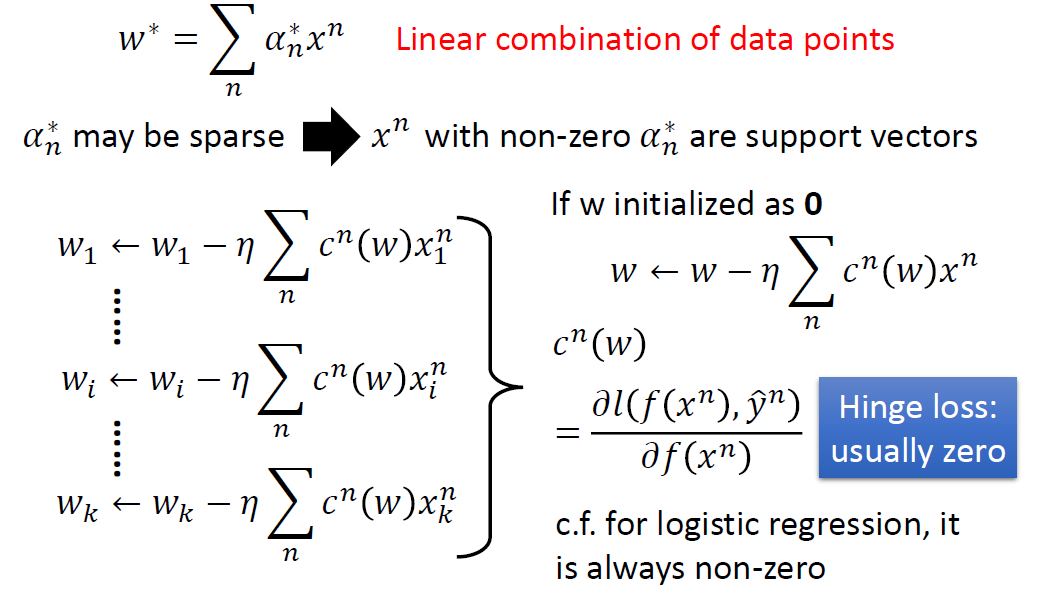
如果对于之前求出的迭代更新的式子,把
线性参数
support vectors就是那些线性参数
这样结合的好处是:不是支持向量的数据点(有可能是outlier),去掉(线性参数
Kernel Trick
改写函数集为Kernel Function
重新表示模型参数为
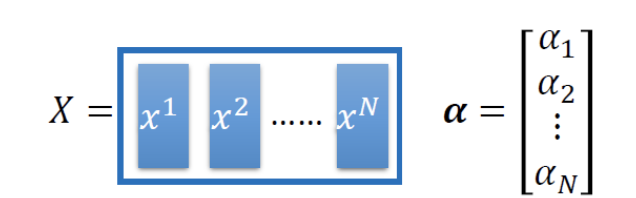
重新表示模型函数集为
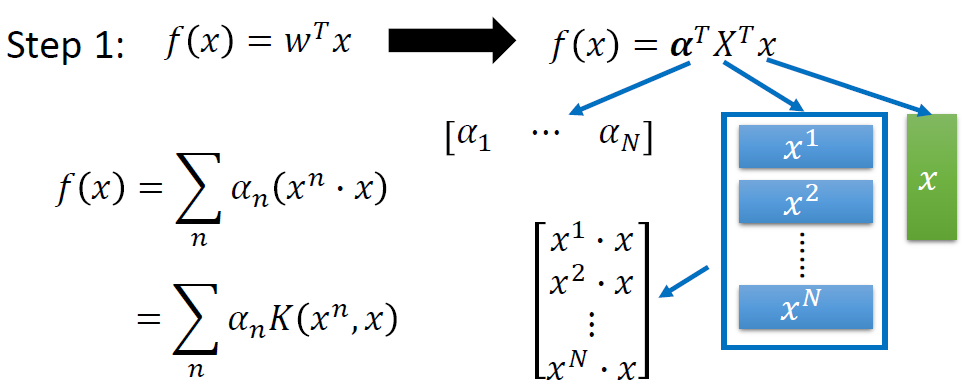
把内积
接下来最小化损失函数,也就是训练目的:找一组
什么时候用Kernel Trick?
不止用在SVM中。当我们对data的表示比较困难,或者说需要对input data用好几个hidden layer做feature transform,这时候Kernel trick is useful when we transform all x to
。 我们需要把feature transform后的多个data vector做inner product,因为做feature transform之后维度变大了,所以运算量很大。
而Kernel Trick告诉我们,你直接算原来的data vector,做inner product再平方就可以了,和上面的过程得出的结果是一样的。
依据核函数的定义方式有很多变化。
Radial Basis Function Kernel
在一个无穷多维的空间做inner product。推导涉及exp函数的泰勒展开。
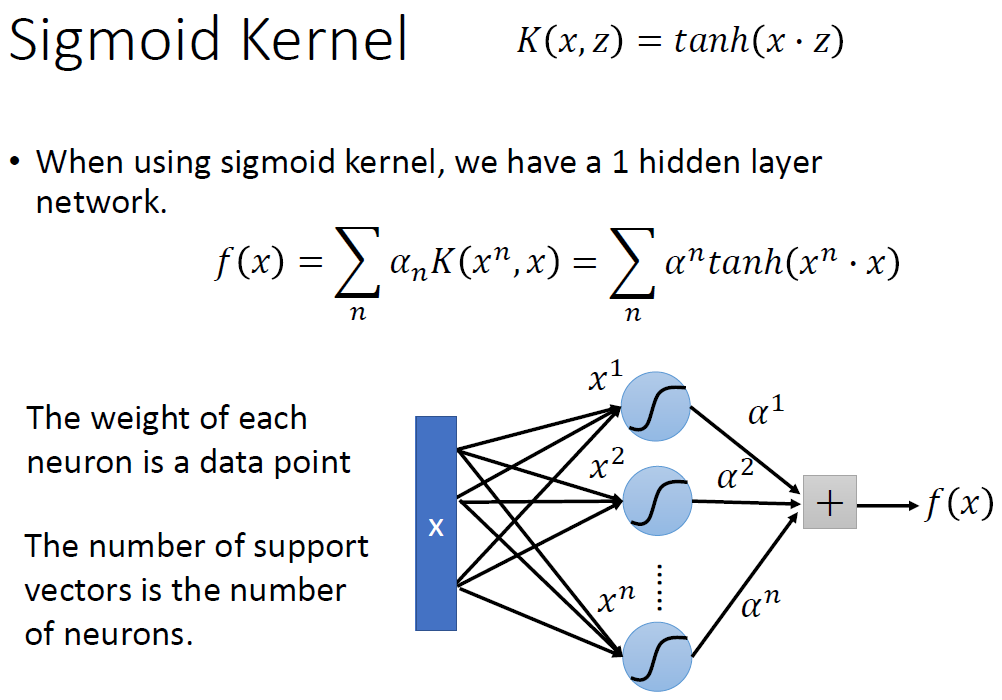
Sigmoid Kernel
每一个函数都可以看作一个Neuron Network。原始数据到第一层neuron的weight就是每一个data point
更多的启发
直接设计Kernel Function,不用理会x和z的的feature。Kernel Function有点类似于把x和z放到高维之后的相似度。
核函数做了什么?我们要找的这个Kernel Function,把x和z放进去,会得出一个value,这个value代表了x和z在高维上的inner product。
什么样的data适合核方法?When x is structured object like sequence, hard to design its feature transformation function
- 本文标题:支持向量机
- 本文作者:徐徐
- 创建时间:2020-11-07 15:10:53
- 本文链接:https://machacroissant.github.io/2020/11/07/svm/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!