
参数说明
$\nabla L(\thetat)
$m{t+1}
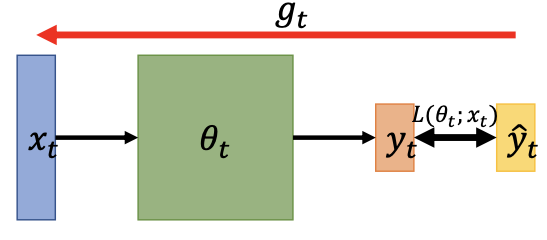
参数迭代方式
on-line:一次用一对input&label算损失函数更新参数
off-line:一次用所有input&label算损失函数更新参数
SGD
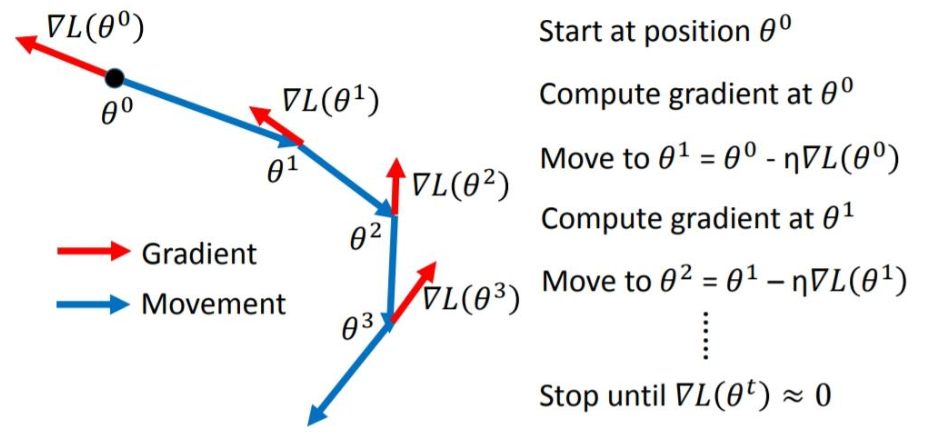
我们要Minimize Loss Function,梯度代表了增加的方向,往梯度的反方向走,就可以走向最小值。
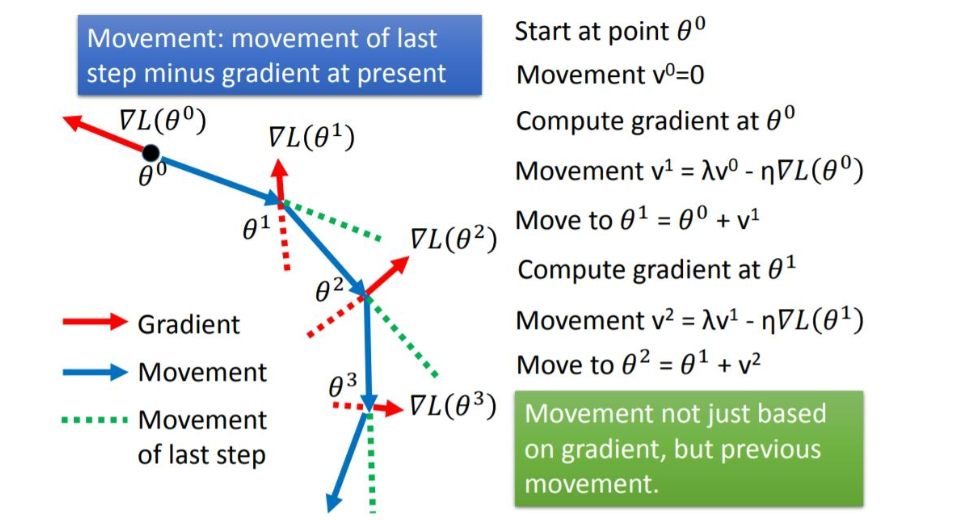
SGDM
定义了一个momentum,初始值为0。本次参数的更新是momentum和上一次迭代参数的矢量和。注意momentum的求解也用到了gradient,并且用lambda考虑了上一次迭代的momentum。
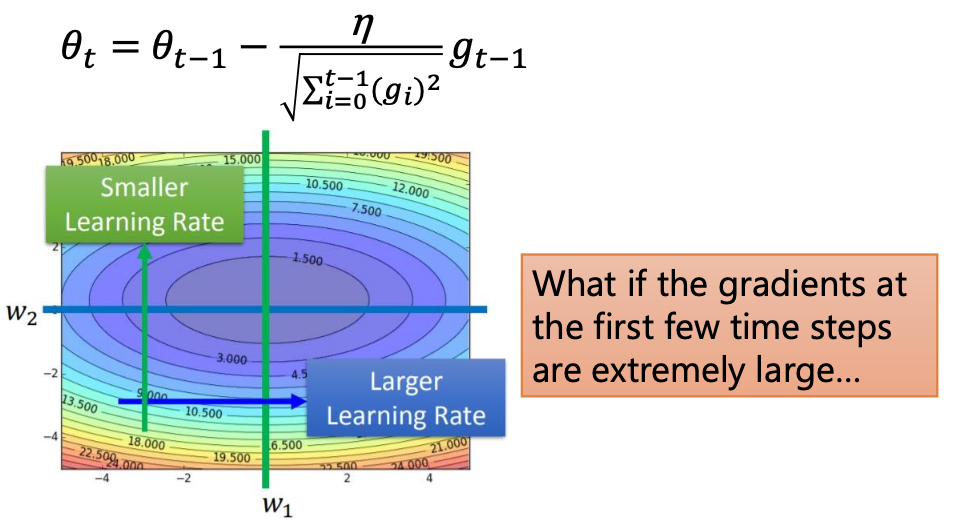
Adagrad
Adagrad就是把SGD的学习率加上了一个分母。如果前几次迭代中gradient值很大的时候,一开始就会一步跨很大,有了分母的约束之后,如果过去的gradient很大的话(代表比较崎岖的地方),就能让每一步走小一点。
问题在于,分母会越来越大,之后每一步的参数更新会越来越小。要是一开始的gradient就很大,那么没几步就不走了。
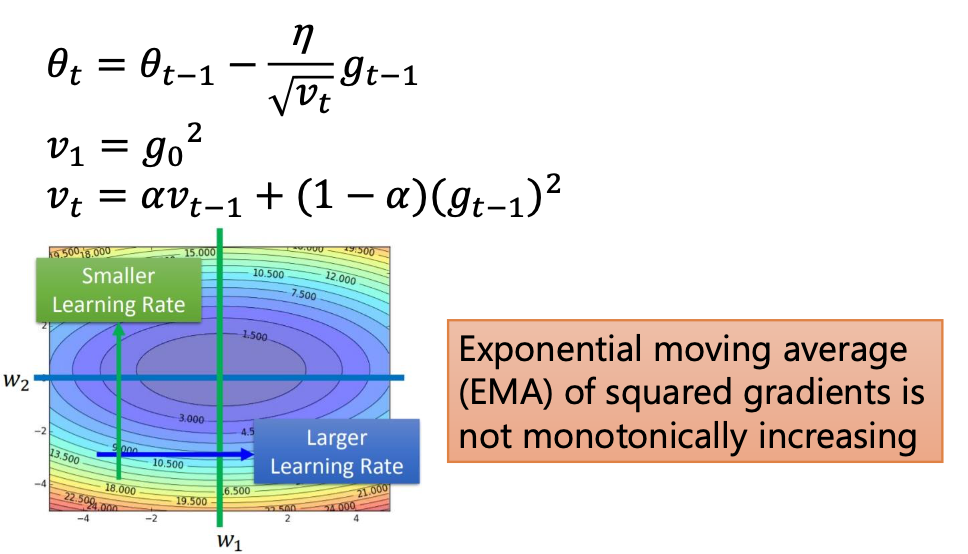
RMSProp
和Adagrad的分母的算法有所不同,同时借用了SGDM的思想。既考虑了gradient,有考虑了momentum,这两者的结合就是下面式子中的v,且用一个参数去权衡这两个的比重,解决了Adagrad的短板。
但是它还是没有办法解决local minima的问题。
Adam
Adam就是SGDM+RMSProp。
$\hat{m}t
类似的,
一个很小的
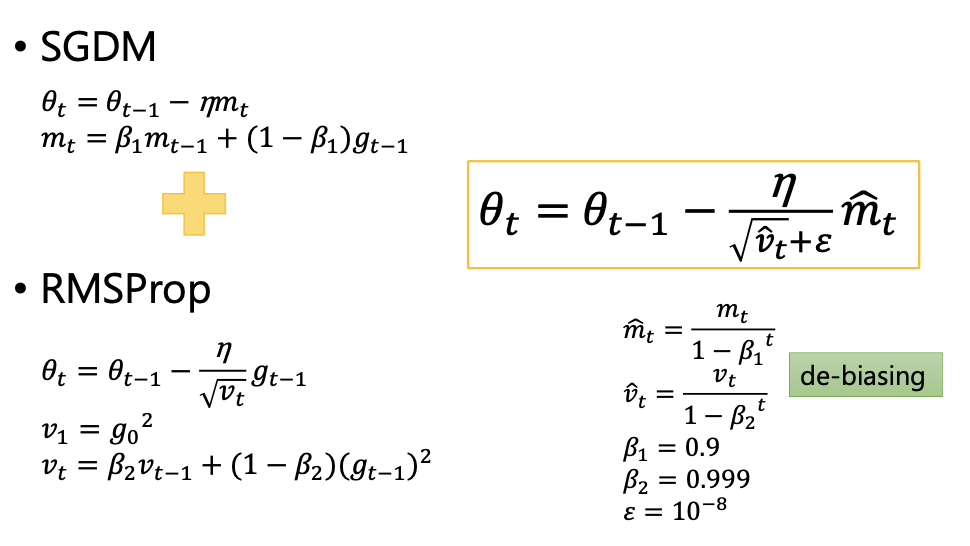
选择算法
Adapative Learning Rate/Adam: fast training/unstable/larger generalization gap虽然能自适应学习率但是在训练后期表现不是很好。
SDGM:stable but slow/better convergence/smaller generalization gap虽然训练起来很慢但是总是很稳定,因为每一步走的都一样长。
Adam优化
SWATS
总的思想:first Adam + After SDGM,结合了Adam和SDGM的长处,追求更好的收敛。
RAdam
总的思想:apply warm-up to the first learning-rate
为什么需要Warm-up?刚开始你去初始化参数的时候并不能知道这个初始化参数是否好,所以一开始做梯度下降,很有可能参数在乱更新,分布的方差很大,更新的大小很乱且方向也很乱 —— distorted gradient。所以一开始就要让走的步
最简单的warm-up就是给参数更新定一个曲线,直线增加4000个update之后曲线下降。
Lookahead
K step forward,1 step back.
Nadam
数学中的Nesterov acclerated gradient/NAG应用到Adam中。
协助优化的技巧
L2 Regularization
在定义loss function的时候一般会添加一个L2 Regularization,他也是关于目标参数的一个函数。在做gradient的时候是否要把L2 Regularization当作gradient的一部分放在momentum和gradient中去?
AdamW&SGDW的方法说做微分求momentum和gradient的时候只考虑没有L2 Regularization的loss function,只在最后更新参数的时候把L2 Regularization的微分结果当作一个weight decay项放在learning rate后面。
增加数据随机性
Shuffling
数据更换顺序,让每一次的gradient都有变化。
Dropout
在训练的时候某一些neuron的输出会被丢掉。
Gradient noise
在算完gradient之后加上一个gaussian noise。
- 本文标题:利用梯度下降法最优化损失函数
- 本文作者:徐徐
- 创建时间:2020-11-08 11:08:19
- 本文链接:https://machacroissant.github.io/2020/11/08/summary-for-loss-function-optimization/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!