
MLE
极大似然估计步骤

就是要让真实数据分布中的每一笔data,通过给定参数的新的分布后,所得到的每一笔data概率之积要最大。
最大化求解的转化

Maximum Likelihood Esitimation = Minimize KL Divergence
Generative Model所定义的distribution PG要和真实数据的Pdata尽可能地相近似。
为了计算PG,我们要做假设,比如分布服从Gaussian Mixture Model,但是一旦模型复杂了,我们就没办法计算PG。
GAN拆解
Gnerator在做什么
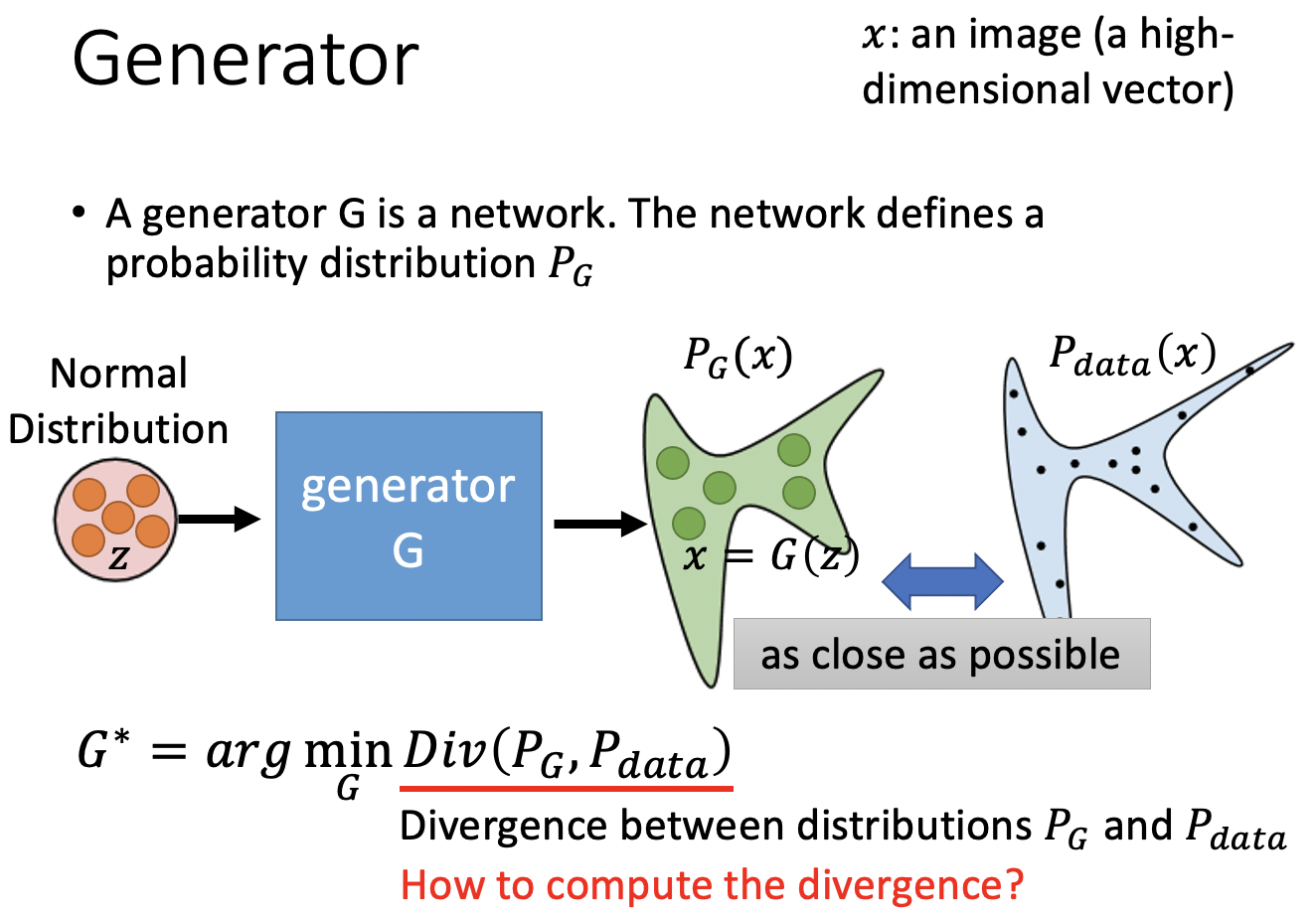
在获得了PG和Pdata也就是两笔数据的分布之后,要最优化Generator。
原始数据分布我们是没有办法完全获得的,这只在理论上现实,因而为了获得分布可以从PG和Pdata中sample一些样本获得样本分布。
要让这两笔数据的差距变小,也就是要最小化这两笔data distribution的Divergence?
从Generator到Discriminator
Discriminator可以告诉我们这些样本所代表的分布之间的Divergence。V(G,D)很小的时候,代表这两个sample data的distribution的divergence很小,很难分辨;V(G,D)很大的时候,代表这两个sample data的distribution的divergence很小,很容易分辨。

证明可求最大值/模型可训练
接下来要证明可以给Example Objective Function for D存在arg max,即可以找到Discriminator的function
对于给定的G,意味着generated data的distribution是确定的。这个时候需要找一个
转换1
也就是要最大化积分表达式中的那个函数。
转换2
用更简单的表达式来替换复杂的符号,
也就是找一个
至此已经找到了能让
Discriminator在做什么
把得到的
从上式我们可以看出:当我们在train一个discriminator,我们就是在衡量我们sample出来的Pdata和PG两个分布之间的Jensen-Shannon Divergence,也是一个binary classifier。

GAN的算法本质上就是在解这个min max problem。
最后Discriminator会怎么样。
它到底是不是一个Evaluation Function,判断generator的output是好还是坏?Discriminator真的会fail掉变成一个水平线吗?这两个问题其实是矛盾的。
(?)最后Discriminator会在有data分布的地方获得比较小的值,没有data分布的地方获得比较大的值。
GAN算法
Theoretically
To find the best G as
具体过程参考GAN Introduction文章。
第一次迭代:
Training D
For Given $G0
Before minimizing loss function, we should determine the best D as $D^
这个过程也就是找一个discriinator能最大化的看到这两个distribution的差异,分辨能力较强,较为严格。
实际上也可能找不到global maxima,可能停在一个local maxima就结束了关于本参数的多次迭代。Can only find lower bound of
.
We use gradient asent several times to maximize the JS Divergence function and thus updating
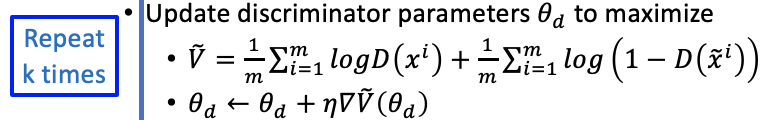
Training G
According to the fixed loss function $L(G) = V(G^0, D_0^)$ at iteration 1, we *use gradient desent just once to minimize the loss function and thus updating
可以看出来,之前maximize和现在minimize的function的表达式都是一样的。但是由于固定了D,现在要优化的式子就没有了上面的第一项。
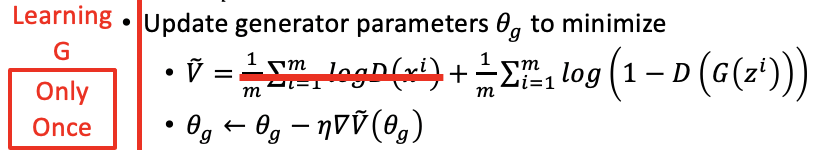
在实际操作过程中objective function for generator是这个样子。
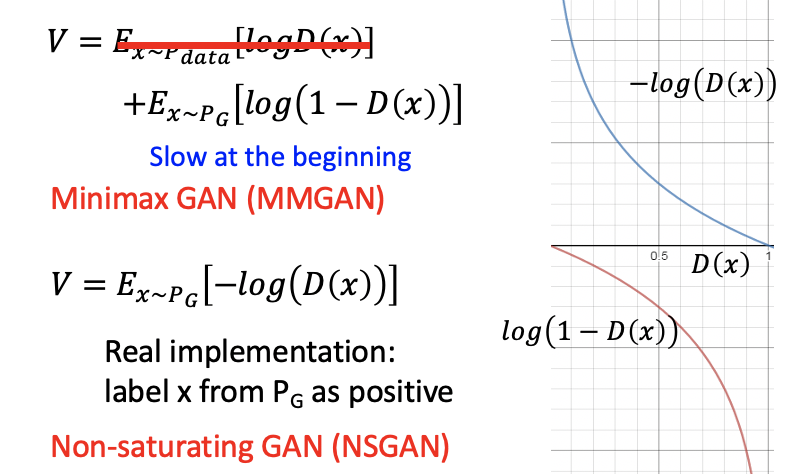
问题是从$V(G_0, D_0^)
V(G_1, D_0^)$,我们希望第一代Generator能够Minimize前面第零代Discriminator计算出来的JS Divergence。 但是当我们update
到 , 整个原来用于衡量JS Divergence的function其实就已经变了,在 处获得的最大值可能已经不是新函数的最大值了,也就是不再是衡量JS Divergence了。 我们要假设在update
到 的时候,参数变动很小,变动前后的function形状变化不大,因此我们只迭代generator一次。
第二次迭代:
For Given $G1
Practically

变动是求期望用Sampling来代替。
Discriminator要maximize的式子的过程就是在做一个binary classifier去minimize cross entropy。
- 本文标题:GAN-theory
- 本文作者:徐徐
- 创建时间:2020-11-12 20:46:03
- 本文链接:https://machacroissant.github.io/2020/11/12/GAN-theory/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!