
What is KDE
Kernel Density Estimation is a way of estimating an unkonwn probability density function given some data, similar to histogram.
Basic idea is you define a kernel function and you center a kernel function $K$ on each sampledata point $xi$, and then you sum these functions together, and then you have a kernel density estimate $\hat{f}(x) = \frac{1}{N}\sum\limits{i=1}\limits^{N} K(x-x_i)$.
Choice of Kernel
Attribute of Kernel
The kernel function $K$ istypically
Non-negative: $K(x) \geq 0$ for every $x$,因为描述的是概率
Symmetric: $K(x) = K(-x)$ for every $x$
Decreasing: $K’(x) \leq 0 $ for every $x$,随着x的增大值靠近0
can be bounded support or not,例如高斯核函数就是渐进0但是不为0,而三角和函数就是直接为0。
Four kinds of kernel
Guassian/Box/Triangle/Triweight
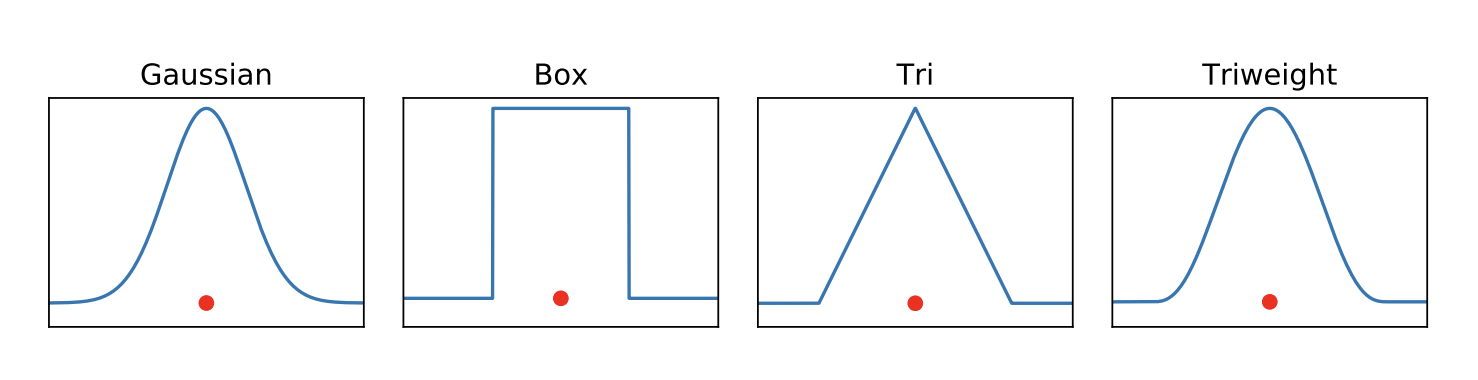
Choice of Kernel is not that important because as data grows large the final function estimation will look as same. Gaussian will be fine.
Choice of Bandwidth
Use $h$ to control for the bandwidth of
感觉bandwidth就是决定了对于每一个数据的核函数的分布函数的分散程度$\sigma$。
Silverman’s rule of thumb
computes an optimal $h$ by assuming that the data is normally distributed.
Improved Sheater Jones(ISJ)
Multimodel, seveal modes, such as two noraml distributions.
Tips
Weighting data
it is possible to add weights $w_i$ to data points $x_i$ by writing
Bounded domains
A simple trick to overcome bias at boundries is to mirror the data.
在分界处间断点如何确定值?把一侧的数据镜像到另一侧,然后两个分布相加后获得的新的original+mirrored distribution在间断点处做切割,做了mirror的那个部分全为概率0,original的部分采用新的original+mirrored distribution。
Extension to d dimensions
An approach to $d$-dimensional estiamtes is to wirte
the choice of norm
The shape of kernel functions in higher dimensions depend on the value of p in the p norm.
As the number of samples grow, the choice of both kernel K and norm p becomes unimportant. The bandwidth H is still important.
Reference
- 本文标题:kernel-density-estimation
- 本文作者:徐徐
- 创建时间:2020-11-14 22:37:52
- 本文链接:https://machacroissant.github.io/2020/11/14/kernel-density-estimation/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!